[딥러닝 기초] 2장 딥러닝 학습의 문제점 - 기울기 소실 문제와 방지 기법

이전 포스팅에서 저희는 딥러닝 모델 학습의 문제점 중 학습 속도 문제를 알아보고 이를 해결한 최적화 알고리즘에 대해 알아보았습니다.

오늘은 딥러닝 모델 학습의 문제점 중 두번째 문제인 기울기 소실문제와 방지 기법에 대해 알아보겠습니다.

 

 

 

- 딥러닝 모델 학습 방법 되짚어보기

 

딥러닝의 역전파(Back Propagation)

 

이전에 배웠듯이 딥러닝 모델은 순전파와 역전파의 반복을 통해 우리가 목표하고자 하는 결과를 도출해내는 모델입니다.

여기서 역전파에 대해 다시 한번 의미를 되짚어보면 나의 목표 target 값과 실제 모델이 예측한 outpu값이 얼마나 차이나는지 구한 후 오차값을 다시 뒤로 전파해가며 변수들을 갱신하는 알고리즘입니다.

 

 

 

- 기울기 소실 문제(Vanishing Gradient)의 발생원인

 

그렇다면 왜 딥러닝 모델에서 기울기 소실 문제가 발생하게 될까요?

 

 

sigmoid 함수의 그래프

 

위 그래프는 활성화 함수 중 하나인 sigmoid함수의 그래프 입니다.

위 그래프를 통해 확인 할 수 있는 사실은 결과 값이 0과 1로 수렴할 경우 무한한 값으로 수렴하기 때문에 기울기가 0인 값을 전달하며 중간 전달값이 사라지는 문제가 발생한다는 것을 확인할 수 있습니다.

 

 

 

- 기울기 소실 문제

 

 

그렇기 때문에 위 사진처럼 딥러닝 모델의 깊이가 깊으면 깊을 수록 기울기의 값이 무수히 작아지고 이로인해 기울기가 소실되는 문제가 반복되며 학습 시간이 엄청 오래 걸리거나 학습 시 오류나 제대로 학습이 이루어지지 않습니다.

 

따라서 인공지능 학자들은 이러한 문제를 해결하기 위해 기존의 활성화 함수(Activation Function) 방식에 변화를 주어 문제를 해결하고자 하였습니다.

 

 

 

- 기울기 소실 문제 해결 방법 : ReLU

 

 

ReLU함수의 그래프와 계단함수의 그래프

 

 

ReLU함수는 앞선 sigmoid함수와는 다르게 입력값이 음수이면 0을 출력하고 양수 값이면 결과값을 그대로 흘려보내는 비교적 간단한 함수임을 우리가 확인할 수 있습니다. 

이를 통해 앞서 설명했던 값이 0과 1로 수렴할 때 무한히 수렴하여 기울기가 0에 가까워지게되는 문제를 해결하게 되었고, 연산이 더욱 간편해지고 Hidden Layer를 깊게 쌓을 수 있게 되었습니다.

 

 

 

- 기울기 소실 문제 해결 방법 : Tanh

 

 

하이퍼볼릭 탄젠트함수 그래프

 

 

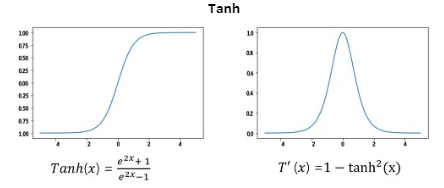
하이퍼볼릭 탄젠트 함수는 쌍곡선 함수라고도 하며, sigmoid 함수 대비 기울기가 작아지지 않는 구간이 넓어서 양수와 음수 모두에서 학습 효율성이 뛰어나게 개선된 활성화 함수입니다. 

심층 신경망에서 시그모이드 함수의 역할이 필요하다면 대안으로써 활용되는 함수여서 Tanh함수와 ReLU함수를 같이 사용한다고 한다면 Tanh함수는 Output Layer에 사용하고, ReLU함수는 내부 Hidden Layer에서 사용하게 됩니다.

하지만 그래프를 보면 Tanh역시 sigmoid함수와 비슷하게 생겼다는 것을 알 수 있습니다. 따라서 ReLU함수처럼 기울기가 0으로 수렴하는 구간이 존재하여 기울기 소실 문제에 대해서는 아주 자유롭지는 않다는 단점이 있습니다.

 

 

 

 

 

 

# 출처

 

엘리스 AI 트랙 7기 - [강의자료]  딥러닝 학습의 문제점

 

https://kevinitcoding.tistory.com/entry/%ED%99%9C%EC%84%B1%ED%99%94-%ED%95%A8%EC%88%98-%EC%A0%95%EC%9D%98%EC%99%80-%EC%A2%85%EB%A5%98-%EB%B9%84%EC%84%A0%ED%98%95-%ED%95%A8%EC%88%98%EB%A5%BC-%EC%82%AC%EC%9A%A9%ED%95%B4%EC%95%BC-%ED%95%98%EB%8A%94-%EC%9D%B4%EC%9C%A0

활성화 함수: 정의와 종류, 비선형 함수를 사용해야 하는 이유